2008-03-28 : GDI+, un GDI 24 bits !

Documentation officielle

GDI+ : http://msdn2.microsoft.com/en-us/library/ms533798(VS.85).aspx

GDI : http://msdn2.microsoft.com/en-us/library/ms536795(VS.85).aspx

La thèse

Soit i=2^24-1-1. Donc i=8 388 607.

Soit j=-2^24-1. Donc j=-8 388 608.

Soit E=[i;j]. Alors E² représente l'ensemble des points du plan adressable par le GDI+ ! Donc GDI+ est un GDI 24 bits, et non pas 32 bits comme on aurait pu le penser. C'est néanmoins une amélioration certaine sur le vieux GDI 16 bits.

La preuve

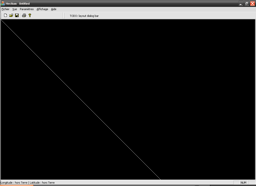
Il suffit de dessiner un segment joignant les points extrêmes de coordonnées (j;j) et (i;i) :

Gdiplus::PointF pC1;

Gdiplus::PointF pC2;

pC1.X = -8388608.0f;

pC2.X = 8388607.0f;

pC1.Y = -8388608.0f;

pC2.Y = 8388607.0f;

Gdiplus::Pen colour(Gdiplus::Color(255, 255, 255, 255));

pGr->DrawLine(&colour, pC1, pC2);

Voici ce que ça donne en images :

Logiciel Héclium - Capture d'écran - Cliquez pour agrandir

Le segment est donc correctement dessiné comme prévu.

Dessinons maintenant un segment à peine plus grand joignant les points extrêmes de coordonnées (j;j) et (i+1;i+1), et en contrôlant le résultat du tracé du segment :

Gdiplus::PointF pC1;

Gdiplus::PointF pC2;

pC1.X = -8388608.0f;

pC2.X = 8388608.0f;

pC1.Y = -8388608.0f;

pC2.Y = 8388608.0f;

Gdiplus::Pen colour(Gdiplus::Color(255, 255, 255, 255));

Gdiplus::Status status = pGr->DrawLine(&colour, pC1, pC2);

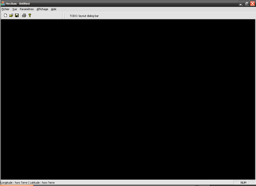
On était en droit de visualiser exactement le même résultat que précédemment (au pixel près !), mais c'est plutôt la plénitude amnésique qui nous attend :

Oui : le néant total ! GDI+ échoue quand les coordonnées sont en dehors du domaine 24 bits. On avait le même type de comportement avec le GDI qui faisait n'importe quoi quand on lui soumettait des coordonnées en dehors du domaine 16 bits.

Problème inquiétant : la variable status conserve la valeur « Ok »...

Autre information : le problème reste identique si on remplace les Gdiplus::PointF par des Gdiplus::Point.

Conclusions

Évidemment, ce type de comportement ne gêne pas beaucoup de programmeurs puisque généralement on cherche à dessiner dans la zone d'affichage, donc généralement à l'intérieur de [0;0]x[2560;1600]. En revanche, dans le cas du logiciel Héclium, les polygones à dessiner ont des sommets dont les coordonnées peuvent être très importantes.

Enfin, la documentation officielle (http://msdn2.microsoft.com/en-us/library/ms536022(VS.85).aspx ) ne dit rien sur ce problème ce qui est anormal.

◄ Retour